正規分布とは?¶
正規分布の確率密度関数は次の式で定義されます。
$$ f(x | \mu,\sigma) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} $$¶
μは平均、σは標準偏差です。円周率π=3.14... と自然対数の底 e=2.718... は定数です。
確率の総和は1です。X=aとX=b(a<b)の間に挟まれた領域は、Xがaとbのあいだになる確率を意味していて、これを次のように書きます。$Pr(a
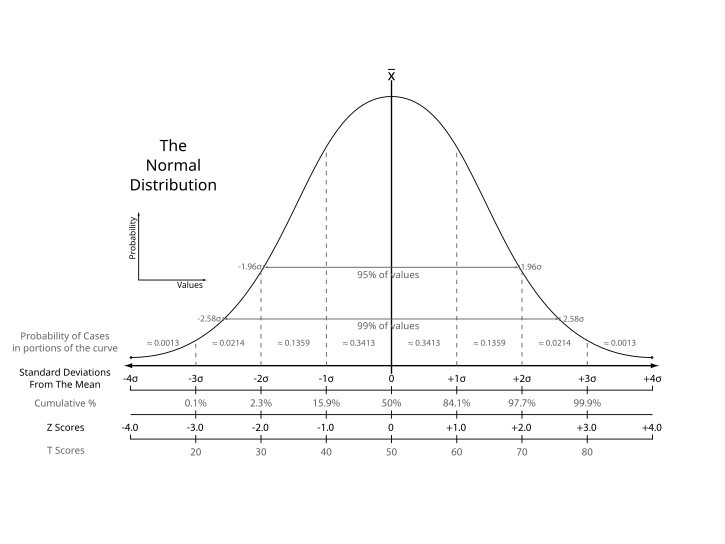
分布の形を見て、正規分布の主な特徴を確認していきましょう。
1.) 左右に裾野を持ちます。
2.) 曲線は左右対称です。
3.) ピークは平均の値です。
4.) 標準偏差が曲線の形を特徴付けます。
- 背が高い分布は、小さな標準偏差のときです。
- 太った分布は、大きな標準偏差のときです。
5.) 曲線のしたの面積(AUC: area under the curve)は1です。
6.) 平均値、中央値、最頻値(mode)がすべて同じです。平均が0、標準偏差が1の標準正規分布では、±1標準偏差に68%、±2標準偏差に95%が含まれ、±3標準偏差までには、全体の99.7%が含まれます。この1,2,3といった数字をz-scoreと呼ぶこともあります。
In [1]:
from IPython.display import Image
Image(url='http://upload.wikimedia.org/wikipedia/commons/thumb/2/25/The_Normal_Distribution.svg/725px-The_Normal_Distribution.svg.png')
Out[1]:
scipyを使って、正規分布を作ってみましょう。
In [3]:
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
# statsライブラリをImportします。
from scipy import stats
# 平均を0
mean = 0
# 標準偏差を1にしてみましょう。
std = 1
# 便宜的に領域を決めます。
X = np.arange(-4,4,0.01)
# 値を計算します。
Y = stats.norm.pdf(X,mean,std)
plt.plot(X,Y)
Out[3]:
numpyを使っても正規分布を作れます。
In [4]:
import numpy as np
mu,sigma = 0,0.1
# 正規分布に従う乱数を1000個生成します。
norm_set = np.random.normal(mu,sigma,1000)
In [5]:
# seabornを使ってプロットしてみましょう。
import seaborn as sns
plt.hist(norm_set,bins=50)
Out[5]:
正規分布は非常に重要な分布なので、多くの情報があります。ここでの導入は、最初の1歩にすぎませんので、是非いろいろと調べてみてください。
1.) https://ja.wikipedia.org/wiki/%E6%AD%A3%E8%A6%8F%E5%88%86%E5%B8%83
2.) http://mathworld.wolfram.com/NormalDistribution.html
3.) http://stattrek.com/probability-distributions/normal.aspx